Philosophie + Mathematik + Musik
Wenn ich mich, allein oder beim Anspielen vor einem Auftritt mit meinem Horn beschäftige stelle ich immer wieder fest, dass das das Erzeugen der Töne für mich immer einen mediatativen Charakter hat.
Sei es das Anspielen des Pedal C, das wie ein tiefes "Ohmmm" anmutet und wie kein anderer Ton tief in meinem Inneren Resonanz schwingt. Oder alle anderen oberen Töne , die sich architektonisch wie Bausteine aneinander reihen, darüber formatieren, so dass die Tonsequenzen am Ende wie eine klassische Brückenkonstruktion anmuten.
Der Mensch sucht schon seit Urzeiten nach einer Weltenformel. die erkärt was "die Welt im Innersten zusammenhält". Doktor Faustus zermartert sich genau, darüber den Kopf und ist bereit für diese Formel sich an den Teufel zu verkaufen.
Leonardo da Vinci sucht im Bild des Menschen "Göttliche" Proportionen , feste mathematische Relationen die vollkommen sind. Er entwickelt die Grundlagen der Ästhetik, die Anwendung in der Architektur und Technik finden.
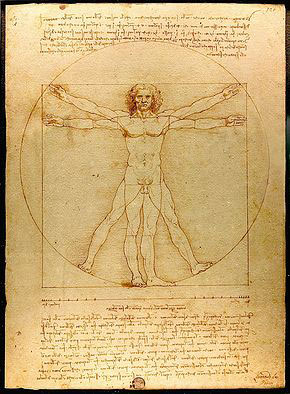
Die Kirchen des Mittelalters sind beispielsweise exakt in diesen Proportionen gebaut und vermitteln daher vielleicht unbewusst eine Eindruck dieser universellen Regelmässigkeit und überirdischen Größe. Aufgrund der Proportionen haben diese Gebäude auch eine hervorragende Akustik, Musik klingt in ihnen besonders schön.
Die folgenden Bilder sind einem Artikel aus dem Internet entnommen, von einem Mann der
sich eingehend mit Harmonie beschäftigt:
http://www.hans-henny-jahnn.de/Der_Harmoniker.html (verlinkter Artikel nicht mehr vorhanden)
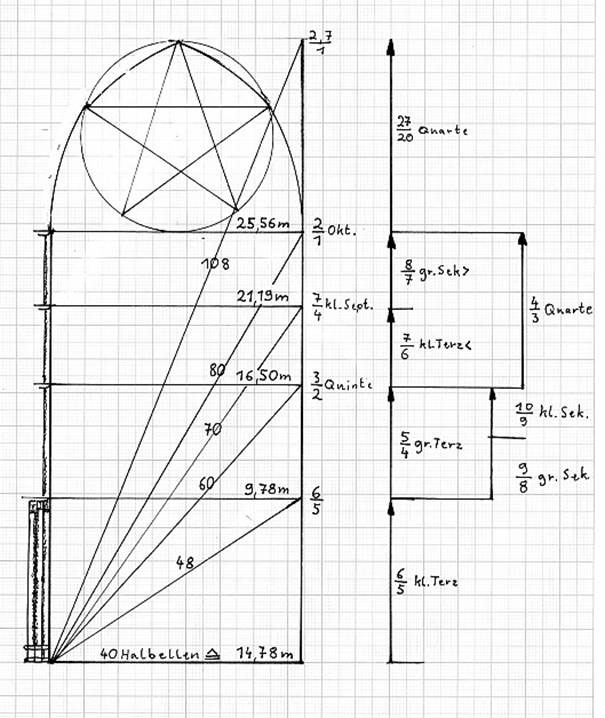
Die Lehre von Ästhetik, der Proportionen und Relationen ist ncht nur ein europäischer Gedanke, gerade ich Fernost prägt er grundlegend die Gedanken der TCM des Feng Shui und auch des buddhistischen Kulturgutes. Man denke an die asiatischen Klangschalen die heiligen buddhistischen Tuben oder auch an das Didgeridoo.
Pythagoras (ca 5oo v Chr) beschreibt zum ersten Mal eine Harmonielehre für die Musik. Er findet heraus, dass bestimmte Töne zueinander harmonisch Klingen oder eben nicht und dass die Freqenzen dieser Töne in genau den selben Proportionen sich verhalten, die später auch universell für die gesamte Lehre der Ästhetik gelten. Akkorde klingen nur gut, wenn sie in den Fequenzen zusammenpassen
Er macht Versuche mit einem Brett auf denen Saiten aufgetragen sind, dem sogenannten Monochord, unterteilt die Saiten und findet mathematische Gesetzmässigkeiten. So klingen beispielsweise der Grundton und die halbe Saite harmonisch , auch der Ton von Grundton und 2/3 Saite. Noch angenehm gilt das Verhältnis Grundton zu 3/4 der Saite. Die Pythagoräer setzen nun 2/3 ins Verhältnis zu 3/4 und erhalten somit eine (2/3 : 3/4) = 9/8 Einteilung usw.
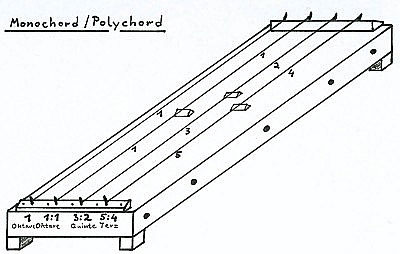
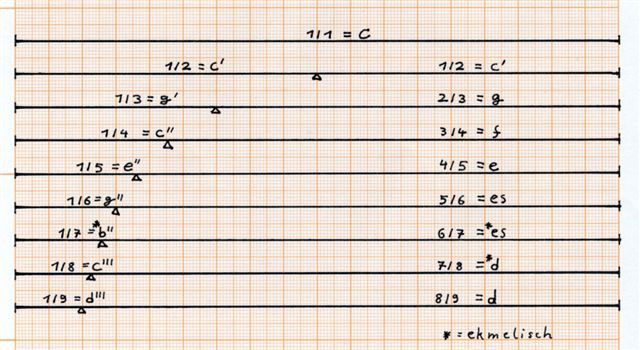
Der Tonaufbau beim Naturhorn entspricht ganz exakt dem pythagoräischen Prinzip. Die Frequenzen der Töne stehen in festen mathematischen Relationen zueinander.
Das erklärt wohl hinreichend die innere Harmonie des Bläsers mit seinem Horn. Er erfühlt und ergründet beim Blasen die fundamentalen Symmetrien mit seinem Lippen und seinem Geist, das Horn schwingt Resonanz, gibt diesen Symmetrien Ausdruck und stellt sie als Klangkörper in den Raum.
Somit kommt es zu einer meditativen Auseinandersetzung mit seinem Instrument ähnlich wie die Stimmung beim Betreten einer altehrwürdigen Kirche.
Dabei erfährt die Ausdehnung des Schalles vom Schalltrichter des Hornes aus auch einer räumliche Dimension ähnlich einer Orgelpfeife. Das physikalische Äquivalent ist dass Wellenlänge reziprok der Frequenz eines Tones ist.
Vielleicht ist es kein Zufall, dass Orgel und Naturinstrumente besonders in alten Kirchen immer wieder Tausende Zuhörer faszinieren.
Diese Besonderheiten gehen leider beim diatonischen Instrument zumindest teilweise verloren, es gibt sie nur beim Naturinstument
